新鲜事¶

pclasso¶

Refer to pcLasso: a new method for sparse regression

set.seed(1234)
n = 100; p = 10
X = matrix(rnorm(n * p), nrow = n)
y = rnorm(n)
library(pcLasso)
fit <- pcLasso(X, y, theta = 10)

predict(fit, X[1:3, ])[, 5]

groups = list(1:5, 6:10)
fit = pcLasso(X, y, theta = 10, groups = groups)

fit = cv.pcLasso(X, y, theta = 10)
predict(fit, X[1:3,], s = "lambda.min")

Emojis in scatterplot¶

References:

library(ggplot2)
library(emoGG)
data("ToothGrowth")
p1 <- geom_emoji(data = subset(ToothGrowth, supp == "OJ"),
                aes(dose + runif(sum(ToothGrowth$supp == "OJ"), min = -0.2, max = 0.2),
                   len), emoji = "1f34a")
p2 <- geom_emoji(data = subset(ToothGrowth, supp == "VC"),
                 aes(dose + runif(sum(ToothGrowth$supp == "OJ"), min = -0.2, max = 0.2),
                     len), emoji = "1f48a")

ggplot() +
    p1 + p2 +
    labs(x = "Dose (mg/day)", y = "Tooth length")

Medians in high dimensions¶

Refer to Medians in high dimensions

marginal median
geometric median
medoid
centerpoint
Tukey median

Laplace distribution as a mixture of normal distributions¶

Refer to Laplace distribution as a mixture of normals

$\int_0^\infty f_{X\mid W=w}(x)f_W(w)dw=\frac{1}{2b}\exp\Big(-\frac{\vert x\vert}{b}\Big)\,.$

Gradient descent as a minimization problem¶

Refer to Gradient descent as a minimization problem

put gradient decent into the optimization framework, then derive

projected gradient descent
proximal gradient methods

Coordinate descent doesn’t always work for convex functions¶

Refer to Coordinate descent doesn’t always work for convex functions

A counterexample:

$z=\max(x,y)+\vert x-y\vert$

Solution to a `sgn` equation¶

Refer to Soft-thresholding and the sgn function

Give a proof of the solution of

$ax-b+c\mathrm{sgn}(x)=0$

where $a>0$ and $c\ge 0$ .

Horvitz–Thompson estimator¶

Refer to Horvitz–Thompson estimator

Perform an inverse probability weighting to (unbiasedly) estimate the total $T=\sum X_i$ .

Illustration of SCAD penalty¶

Refer to The SCAD penalty

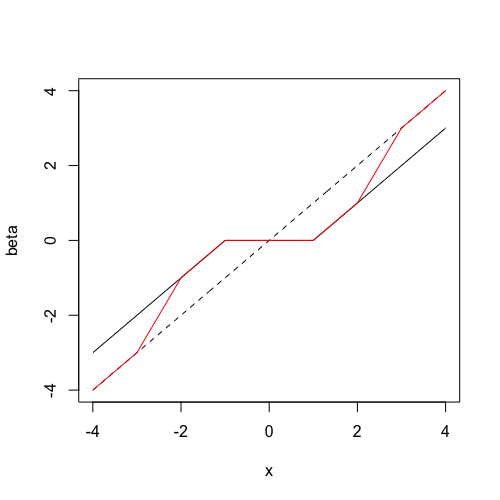
The dotted line is the $y=x$ line. The line in black represents soft-thresholding (LASSO estimates) while the line in red represents the SCAD estimates.

Leverage in Linear regression¶

Refer to Bounds/constraints on leverage in linear regression

The leverage of data point $i$ is the $i$ -th diagonal entry of the hat matrix.

Modification to fundamental sampling formula¶

Refer to Inverse transform sampling for truncated distributions

We can draw sample $X\sim F$ conditional on $X\ge t$ .

Borel’s Paradox¶

Retire Statistical Significance¶

A petition

EM estimation for Weibull distribution¶

$f_k(x) = k x^{k-1} e^{-x^k} \quad x >0$

Refer to EM maximum likelihood estimation for Weibull distribution

A little confused about the answer

Power method for top eigenvector¶

Power method for obtaining the top eigenvector

Generalized Beta Prime¶

This distribution, characterized by one scale and three shape parameters, is incredibly flexible in that it can mimic behavior of many other distributions.

GB2 exhibits power-law behavior at both front and tail ends and is a steady-state distribution of a simple stochastic differential equation.

Julia Set¶

在复杂动力学里，Julia集是个著名的“混沌”行为的集（与之对应的是Fatou集，“非混沌”集）

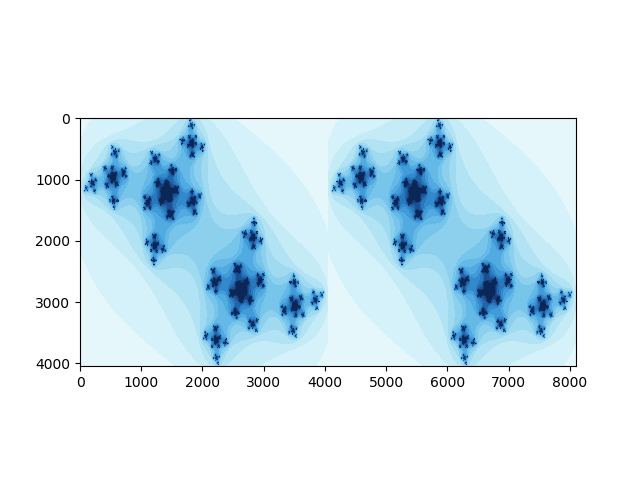
References:

陈素数¶

陈素数是陈景润素数的简称，特指符合陈氏定理的素数，即：如果一个素数 p 是陈素数，那么 p+2 是一个素数或两个素数的乘积，它是素数的子集，陈素数有无穷多个，已经被陈景润证明。

source: https://zh.wikipedia.org/wiki/%E9%99%88%E7%B4%A0%E6%95%B0

陈素数数列：A109611@OEIS

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 47, 53, 59, 67, 71, 83, 89, 101, 107, 109, 113, 127, 131, 137, 139, 149, 157, 167, 179, 181, 191, 197, 199, 211, 227, 233, 239, 251, 257, 263, 269, 281, 293, 307, 311, 317, 337, 347, 353, 359, 379, 389, 401, 409

孪生素数¶

孪生素数（英语：twin prime），也称为孪生质数、双生质数，是指一对素数，它们之间相差2。例如3和5，5和7，11和13，10016957和10016959等等都是孪生素数。

与之相关的，两者相差为1的素数对只有 (2, 3)；两者相差为3的素数对只有 (2, 5)。

孪生素数猜想：孪生素数有无穷多个。这个猜想至今仍未被证明。

2013年5月14日，《自然》杂志报道，数学家张益唐证明存在无穷多个素数对相差（上界）都小于7000万。论文已被《数学年刊》（Annals of Mathematics）接受。截至2014年10月9日, 素数对之差被缩小为 <=246。另见果壳科普：孪生素数猜想，张益唐究竟做了一个什么研究？

minimax @ 知乎¶

在统计中，什么是minimax risk 呀，这个和通常的收敛速度有什么区别？

随机矩阵¶

李军@zhihu - 随机矩阵理论综述

本文，我们来谈谈随机矩阵理论的历史、已有的理论成果以及一些新的研究探索。为了方便更多不同学科背景，不同知识层级的同学学习RMT，本文内容尽量循序渐进。由于内容众多，这里我只列出，具体内容、参考文献以及Python实现(本人一个个细致推敲实现，但很多分布仍未进行很好的normalization)，请见我的Github。由于时间有限，不免有很多内容没有讲到，而且RMT理论及应用涉及众多学科领域，更难完全罗列介绍，本文只选择一些重要成果进行介绍，只对部分内容进行了较细致分析，更多的理论推导请查阅相关文献。

二元二次函数最值¶

参考二元二次函数

Three leading medical journals¶

the Journal of the American Medical Association,
the Lancet, and
the New England Journal of Medicine

Two Most Popular Creative Commons (CC) licences¶

CC-BY-NC (Attribution-NonCommercial): letting others remix, tweak and build up your work non-commercially
CC-BY-NC-SA (Attribution-NonCommercial-ShareAlike): letting others remix, tweak and build upon your work non-commercially, and the person also need to distribute their contributions under the same licence as the original.

License¶

普通许可：non-exclusive license
排他许可：sole license
独占许可：exclusive license
分售许可：sub-license
交叉许可：cross license

dogleg method vs `dodge` option¶

dodge option in StatsPlots.jl

groupedbar(rand(10,3), bar_position = :dodge, bar_width=0.7)

while “dogleg method” refers to an approach in optimization.

比特币¶

比特币简明教程